马尔可夫链

马尔可夫链（Markov Chains）^[1]是具有马尔可夫性质的离散时间随机过程。该过程在给定当前知识或信息的情况下，只有当前的状态用来预测将来，过去（即当前以前的历史状态）对于预测将来（即当前以后的未来状态）是无关的，即t+1时刻系统状态的概率分布只与t时刻的状态有关，与t时刻以前的状态无关。在马尔可夫链的每一步，系统根据概率分布，可以从一个状态转移到另一个状态，也可以保持当前状态。

设马尔可夫链从状态P_i转移到P_j的转移概率为p_ij，则有一步转移概率矩阵：

转移概率矩阵是这样写的：竖排是起始状态，由小到大排列；横排是到达状态，由小到大排列。n步转移概率矩阵：P(n)=Pⁿ。

正则链的极限分布是方程组

的唯一解。

现在讨论一个由单元件构成的简单系统，该元件有两种状态：工作状态（X＝0），简称“0状态”；停运状态（X＝1），简称“1状态”。工作状态由于故障而转移到停运状态，停运状态由于修理而恢复到工作状态，状态转移图如下：

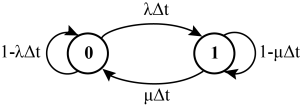
上图中，λ为故障率（在时刻t以前正常工作，在t后单位时间里发生故障的条件概率密度），μ为修复率（在时刻t以前故障，在t后单位时间里修复的条件概率密度）。

转移概率矩阵为：

转移密度矩阵A为：

平衡状态概率是方程组

的唯一解。

可解得该简单系统处于工作状态概率π₁和停运状态概率π₂分别为：