浦丰投针问题（Buffon’s Needle Problem）

浦丰投针问题（Buffon’s Needle Problem）是几何概率的经典问题之一，由George-Louis Leclerc和Comte de Buffon于1777年提出——平面上画有等距离为D（D>0）的无限多条平行线，向此平面投掷一根长度为L（L≤D）的针，则该针与任一平行线相交的概率P_cut为：

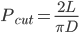
重复进行投掷的试验，记下试验总次数N_d和针与平行线相交的次数N_c，则利用以上公式可以近似求得圆周率π：

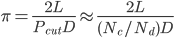
上式是π的有偏估计量。

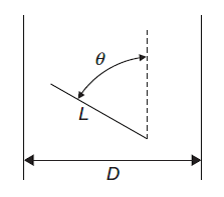
考虑D≥L的情况，如上图所示，当针与垂直线的夹角为θ时，针投影在水平线上的长度为Lsin(θ)，且由于针头处在两平行线中任意位置是等概率的，所以针以夹角θ与左平行线相交的概率为P_cut(θ)=Lsin(θ)/D，针与垂直线成夹角θ的概率为dθ/π，因此，随机投掷的针与平行线相交的概率为：

上面结论也可以使用联合概率密度法证明^[1]。
考虑D<L的情况，令。
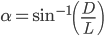当θ∈(0, α)时，针与平行线相交的概率为：

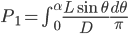
当θ∈(α, π/2)时，针与平行线以概率1相交：

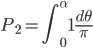
因此，当D<L时，随机投掷的针与平行线相交的概率为：

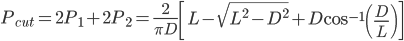
Laplace于1812年提出了浦丰投针问题的另一个变体^[2]：

当长为L的针随机投掷到由边长分别为C和D的矩形组成的平面里，则该针与矩形至少一边相交的概率是多少？

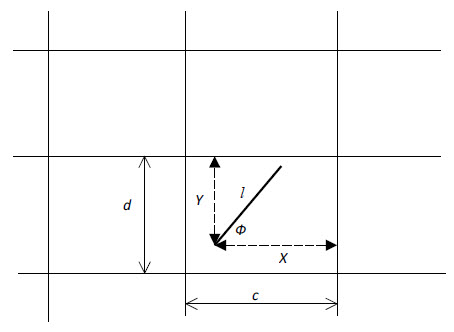
令针的基点与下一条垂直线的水平距离为X，与下一条水平线的垂直距离为Y，针与水平方向的夹角为Φ。X、Y、Φ分别在(0, C)、(0, D)、(0, π/2)均匀分布。当X<LcosΦ时，针与一条垂直线相交，其概率为：

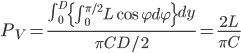
类似地，当Y<LsinΦ，针与一条水平线相交，其概率为：

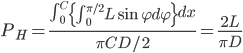
当X<LcosΦ且Y<LsinΦ时，针均与垂直线和水平线相交，其概率为：

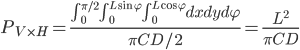
因此，针与垂直线或者水平线相交的概率为：

当C→∞时，由上式可得：

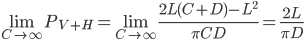
与（\ref{F1}）结果一样。

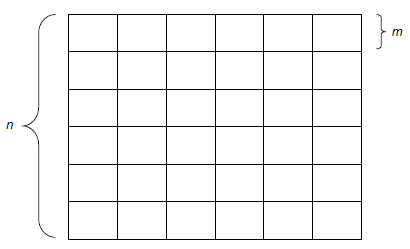
既然我们可以通过几何概率的方法估计圆周率π的值，那么能否通过几何概率的方法估计指数e的大小？Nahin于2000年给出了以下方法^[2]。想像一个n×n的大正方形，它由相同的m×m的小正方形组成，如下图所示。我们选择这样的m值，可以令n/m为正整数，则小正方形的个数为N=n²/m²。

现有N个飞镖随机地扔向大正方形，令X为某一个小正方形里的飞镖数量，则X服从二项分布，X~B(N,1/N)，且有：

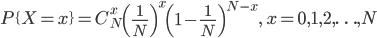
小正方形没有飞镖的概率为：

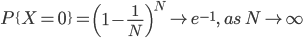
我们可以如下估计e的值：令m很小，则N很大，当N个飞镖扔完后，没有飞镖的小正方形个数为s，则s/N≈1/e，得e≈N/s，其中N/s是e的有偏估计量。