Collecting Coupons: Coupons in cereal boxes are numbered 1 to 5, and a set of one of each is required for a prize. With one coupon per box, how many boxes on the average are required to make a complete set?
这是《Fifty Challenging Problems in Probability with Solutions》书中的第14个题目[1]。在第一个盒子中,我们得到其中一个数字,在下一个盒子中得到另一个数字的概率为4/5,根据《Trials Until First Success》讨论的结果,得到第二个新的数字平均需要1/(4/5)=5/4个盒子,第三个数字平均再需要1/(3/5)=5/3个盒子,第四个数字需要5/2个盒子,第五个需要5/1个盒子。因此,平均需要的盒子总数为:
5(1/5 + 1/4 + 1/3 + 1/2 +1) ≈ 11.42
一般地,对于有N个不同的数字,每个数字出现的概率是均等的,则N个不同数字全都出现时所需要的总次数平均来说等于:
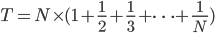
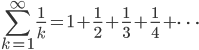 称为调和级数[2],是一个发散级数,其第n个部分和(第n个调和数)的值为:
称为调和级数[2],是一个发散级数,其第n个部分和(第n个调和数)的值为: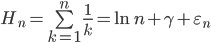
其中γ是欧拉-马歇罗尼常数,约等于0.5772,而εn约等于1/2n,并且随着n趋于正无穷而趋于0。这个结果由欧拉给出。
对于开始的例子,5(ln5 + 1/10 + 0.5772) ≈ 11.43,与11.42非常接近。
考虑某一种包装零食,里面有一张水浒传人物的卡片,那么,要集齐108张不同人物的卡片,平均来说,需要购买该零食的包装数为:
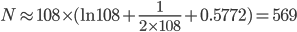
参考:
[1] http://goo.gl/7dOuk
[2] http://zh.wikipedia.org/wiki/调和级数
[1] http://goo.gl/7dOuk
[2] http://zh.wikipedia.org/wiki/调和级数
Speak Your Mind