一、首次出现正面时抛掷次数的平均值E(N)。
令Y=1表示第一次掷硬币的结果是正面,Y=0表示第一次掷硬币的结果是反面,则:
E(N) = E(N|Y=0) × P(Y=0) + E(N|Y=1) × P(Y=1)
=[1 + E(N)] × (1-p) + 1×p
=1 + (1-p) × E(N)
所以:E(N) = 1/p
另一种方法是使用吸收马尔可夫链,以硬币处于正面的状态为吸收状态,易得标准形式的转移矩阵为:

则有:N = (I-B)-1 = [1-(1-p)]-1 = 1/p
即初始为反面时,平均还需要掷1/p次才能得到正面,则有:
E(N) = (1-p)(1+1/p) + 1×p = 1/p
二、首次出现连续k次正面的抛掷次数的平均值E(Nk)
很明显,由第一问可知:E(N1) = 1/p
求解首次出现连续2次正面的抛掷次数的平均值:
1、当第1次掷到反面时,平均需要1+E(N2)次;
2、当第1次掷到正面时,分两种情况:
a)当第2次掷到正面时,这时只需要2次则掷到连续2次为正面;
b)当第2次掷到反面时,则平均需要2+E(N2)。
综上可得:
E(N2) = [1 + E(N2)]×(1-p) + p×p×2 + [2 + E(N2)]×p×(1-p)
上式解得:E(N2) = (1+p) / p2
进一步有:E(N3) = (1+p+p2) / p3
猜想可用数学归纳法解得:
第二问2013.5.15更新:
在看[1]的第七章《更新理论及其应用》过程中,无意中发现了同一个例子,该书中的求解过程更简洁:
通过对首次出现反面的次数取条件,可得:

求解E(Nk)得到

经过化简,可得

三、抛掷N次时,至少得到1次为正面的概率P(N1)
该概率即为(1-没有出现硬币正面的概率),即P(N1) = 1-(1-p)N
四、抛掷N次时,至少出现1次连续2次为正面的概率P(N)2
P(N)2 = P{剩余N-1次中至少出现1次连续2次为正面|第一次为反面}
+ P{剩余N-2次中至少出现1次连续2次为正面|第一次为正面,第二次为反面}
+ P{*|第一次为正面,第二次为正面}
= (1-p)×P(N-1)2 + p×(1-p)×P(N-2)2 + p×p×1
容易得:P(1)2 = 0 ; P(2)2 = p2
根据上面的递推公式可得:
P(3)2 = -p3 + 2p2
P(4)2 = -2p3 + 3p2
P(5)2 = p5 - p4 - 3p3 + 4p2
似乎得不到P(N)2的解释式……
五、抛掷N次时,至少出现1次连续k(1≦k≦N)次为正面的概率P(N)k
很明显,当k=1时,即为第三问,即P(N)k|k=1 = P(N1) = 1-(1-p)N ;
当k=2时,即为第四问,即P(N)k|k=2 = P(N2) 。
P(N)k的通式博主仍未想出,有待以后解决……
如若对第四问的推导式稍微放宽一下:
P(N)2 = P{剩余N-2次中至少出现1次连续2次为正面|第一次为反面}
+ P{剩余N-2次中至少出现1次连续2次为正面|第一次为正面,第二次为反面}
+ P{*|第一次为正面,第二次为正面}
= (1-p)×P(N-2)2 + p×(1-p)×P(N-2)2 + p×p×1
可解得:P(N)2 = 1-(1-p2)N/2
与第三问的结果对比可发现通式:P(N)k = 1-(1-pk)N/k
其中,隐含的条件是N能被k整除。
这个通式的结果比实际的偏小,如求抛掷4次至少出现1次连续2次为正面的概率时,该通式没有考虑类似如下的情况:[反,正,正,反]。由通式计算的概率为7/16,而实际为8/16。一般情况下,对于求抛掷N次至少出现1次连续k次为正面的概率时,通式没有包含的情况为:第1次为反面,第2次为正面,第3次为正面,第4~(N-3)次中没有出现连续k次为正面。
第五问2017.5.18更新:
以一个例子说明解法:抛掷1000次硬币,求连续出现10次或以上正面的概率。
(1)吸收马尔可夫链解法
以出现连续正面的次数作为划分状态空间的依据,则可将状态空间划分为11种。状态0表示没有出现正面(即抛出反面),以0.5的概率达到状态1(抛出正面),以0.5的概率停留在状态0(抛出反面);状态1表示出现连续1次正面,以状态2表示出现连续2次正面……状态10表示出现连续10次正面,且状态10为吸收态。那么问题转化为,在1000次抛硬币的过程中,达到状态10的概率是多少。这是一个马尔可夫过程。将以上过程用状态空间转移图来表示,如下图所示:
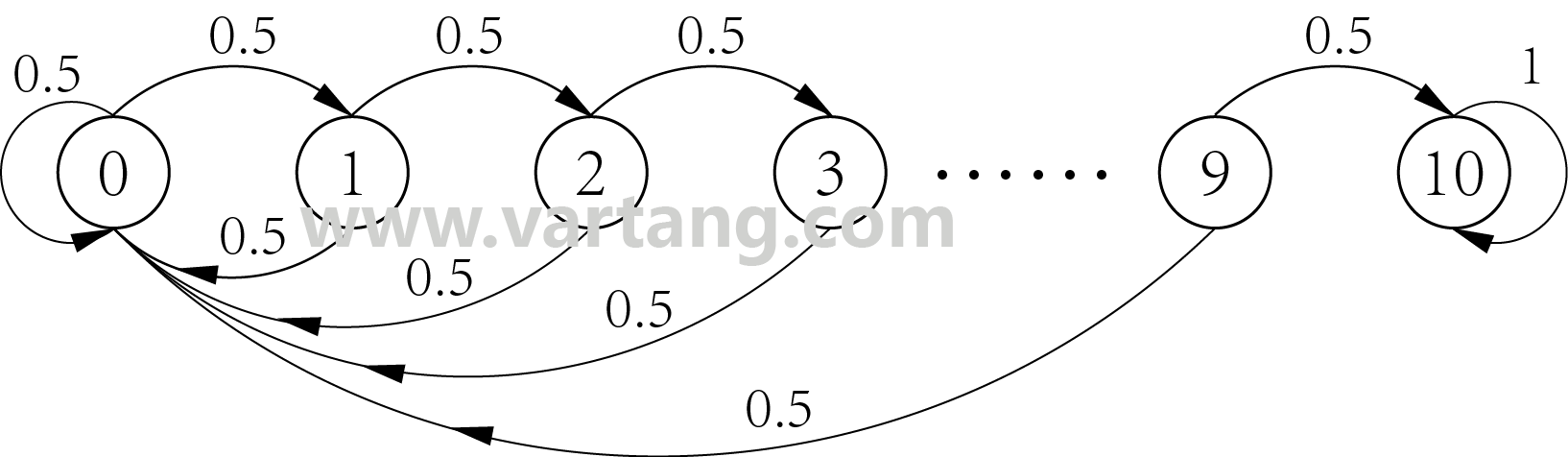
编写程序计算一下达到状态10的概率:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# -*- coding: utf-8 -*- import numpy as np # 状态转移矩阵 # 第1行代表从状态0(没有正面)转移到其它状态的概率 # 第11行代表从状态10(连续10次正面)转移到其它状态的概率,状态10为吸收态 P = np.array([[1/2, 1/2, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1/2, 0, 1/2, 0, 0, 0, 0, 0, 0, 0, 0], [1/2, 0, 0, 1/2, 0, 0, 0, 0, 0, 0, 0], [1/2, 0, 0, 0, 1/2, 0, 0, 0, 0, 0, 0], [1/2, 0, 0, 0, 0, 1/2, 0, 0, 0, 0, 0], [1/2, 0, 0, 0, 0, 0, 1/2, 0, 0, 0, 0], [1/2, 0, 0, 0, 0, 0, 0, 1/2, 0, 0, 0], [1/2, 0, 0, 0, 0, 0, 0, 0, 1/2, 0, 0], [1/2, 0, 0, 0, 0, 0, 0, 0, 0, 1/2, 0], [1/2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1/2], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]]) # 初始状态概率,初始时处于状态0(没有正面),概率为1 t = np.array([1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]) for i in range(1000): t = t@P # 打印迭代1000次后,处于状态10的概率 print(t[10]) |
结果是0.385449752412
(2)迭代法
a)当N=0~9时,抛出连续10次正面的概率为0;
b)当N=10时,抛出连续10次正面的概率为 ;
;
c)当N≥11时,设抛出连续10次正面的概率记为P(N),该情况可分为两种:
1、第1~(N-1)次已抛出连续10次正面,概率为P(N-1);
2、第1~(N-1)次未抛出连续10次正面,当第N次为正面时,得到连续10次正面。则第(N-10)次为反面,第(N-9)~N次(共10次)为正面,第1~(N-11)次没有抛出连续10次正面。这种情况的概率为 ;
;
故得到当N≥11递推公式:
可得P(N)=0.38545
[1] Ross, Introduction to Probability Models (中文版《应用随机过程:概率模型导论》).
Speak Your Mind