以下的第一个匹配问题摘自[1]:
问题:假如你有一个装了n个无差别的球的罐子,每个球分别贴了1,2,3,…,n的标签。每次取出一个球直至所有球均取出,那么,至少有1个球的取出顺序与它的标签一致的概率是多少(例如,标签为2的球是第2个取出来的)?
解答 n个球有n!种排列顺序,假设在某一排列中第j个元素代表第j个取出的球。令Pj(j=1,2,…,n)代表某一给定的排列的第j个取出的球的标签为j,并且令Aj代表具有属性Pj的排列的集合。那么,至少有1个球的取出顺序与它的标签一致的排列的数量Ln为

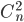 种这样的排列,以此类推,则有
种这样的排列,以此类推,则有
因此,至少有1个球的取出顺序与它的标签一致的概率是
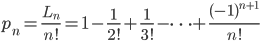
如果求的不是至少有1个球的取出顺序与它的标签一致的概率,而是恰好有r个球的取出顺序与它的标签一致的概率呢?这个第二个匹配问题的讨论在[2]。
首先枚举n=1,2,3,4时的概率,如下表:
| 匹配数目 | 0 | 1 | 2 | 3 | 4 |
| n=1时的概率 | 0 | 1 | |||
| n=2时的概率 | 1/2 | 0 | 1/2 | ||
| n=3时的概率 | 2/6 | 3/6 | 0 | 1/6 | |
| n=4时的概率 | 9/24 | 8/24 | 6/24 | 0 | 1/24 |
同时注意到,每一行的概率和为1。
令P(r|n)为恰好有r个球的取出顺序与它的标签一致的概率。我们可以通过令某r个相匹配且其余不匹配而得到恰好有r个匹配,例如,前r个匹配而剩余的n-r个不匹配的概率为
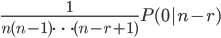
然而,有
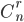 种情况可以得到恰好有r个匹配,因此
种情况可以得到恰好有r个匹配,因此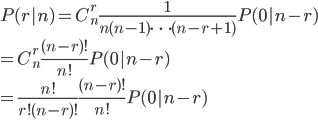
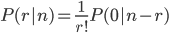
对于r=n的情况,有P(n|n)=1/n!,因此我们可以拓展一下,令P(0|0)=1。
检验一下n=4, r=2时公式(\ref{F2})的正确性,代入公式(\ref{F2})可得
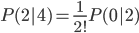
由上面的表格可知,P(2|4)=6/24, P(0|2)=1/2
因此6/24=1/2*1/2=1/4。
我们可以根据公式(\ref{F2}),通过逐渐增加n,一步一步求得P(0|1)、P(0|2)、P(0|3),但无法得出P(0|n)的通式。有时候通过求差会有帮助。根据上面的表格,求P(0|n)-P(0|n-1)的值:
P(0|1) - P(0|0) = 0 – 1 = -1 = -1/1!
P(0|2) - P(0|1) = 1/2 – 0 = +1/2 = +1/2!
P(0|3) - P(0|2) = 2/6 – 1/2 = -1/6 = -1/3!
P(0|4) - P(0|3) = 9/24 – 2/6 = +1/24 = +1/4!
P(0|2) - P(0|1) = 1/2 – 0 = +1/2 = +1/2!
P(0|3) - P(0|2) = 2/6 – 1/2 = -1/6 = -1/3!
P(0|4) - P(0|3) = 9/24 – 2/6 = +1/24 = +1/4!
因此,推断有
P(0|n-r) – P(0|n-r-1) = (-1)n-r/(n-r)!
把所有的求差值相加,可得
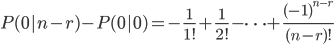
又由于P(0|0)=1/0!=1,上式可变为
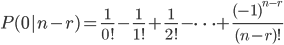
把公式(\ref{F3})代入公式(\ref{F2}),可得
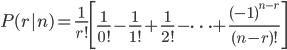
当n-r很大时,公式(\ref{F4})可以近似为
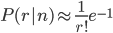
当n充分大时,没有匹配的概率(r=0)约为
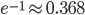 。
。
参考:
[1] Problem 7, Classic Problems of Probability. Wiley, 2012.
[2] Frederick Mosteller, Fifty Challenging Problems In Probability With Solutions. Addison-Wesley, 1965.
[1] Problem 7, Classic Problems of Probability. Wiley, 2012.
[2] Frederick Mosteller, Fifty Challenging Problems In Probability With Solutions. Addison-Wesley, 1965.
[...] 对比公式(ref{F1})和(ref{F2})可得,X=sumlimits_{i=1}^{n}{{{X}_{i}}}的分布可近似为lambda =sumlimits_{i}{{{p}_{i}}}的泊松分布。对于参数为n和p的二项分布,sumlimits_{i}{{{p}_{i}}}=np。 当X的每次试验Xi之间并不相互独立、但相关性较弱时,X仍可近似为lambda =sumlimits_{i}{{{p}_{i}}}的泊松分布。在《匹配问题》一文中,令Ai表示第i个标签匹配,有 [...]