生日问题（Birthday Problem）

生日问题^[1-2]是指在随机选择的一群人当中有两人的生日相同的概率。如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%；对于60或者更多的人，这种概率要大于99%。计算与此相关的概率被称为生日问题，在这个问题之后的数学理论已被用于设计著名的密码攻击方法：生日攻击。

假设有n个人在同一房间内，不考虑特殊因素，例如闰年、双胞胎，并且假设一年365日出生概率是均匀分布的。首先计算每个人的生日日期都不同的概率为：

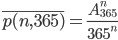
则有两个人在同一日出生的概率为：

n≧365时，p(n,365)=1；当n=23时，p(23,365)大约是0.507。

作为对比，房间中n个其他人中与特定人（比如自己）有相同生日的概率为：

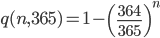
当n=22时概率只有大约0.0586，约等于1/17。

根据泰勒级数展开，有：

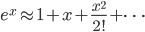
对于x<<1，则有：e^x≈1+x
则公式（\ref{Pn365}）可写成：

进一步泛化，假设有n个人，每一个人都随机地从N个不同的数中选择一个数，则有两个人选择了相同数字的概率为：

当n≧N时概率为1。

反过来，当有两个人选择了同样的数字的概率为p时，需要的人数为：

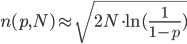
生日问题的另外一个泛化就是求当有m个等可能日期时，在n个人中至少有两人的生日相差k天的概率。其通式为^[3]：

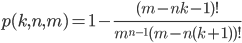
那么，2个人生日相同、相差1天、2天……等的概率大于50％时，需要的人数如下表所示：

生日相差天数	需要的人数
0	23
1	14
2	11
3	9
4	8
5	8
6	7
7	7

因此，在随机的7个人当中，很有可能其中2个人的生日相差在一个星期之内。

《Fifty Challenging Problems in Probability with Solutions》^[4]书中第31~33题讨论了生日问题。