在读Ross的《Introduction to Probability Models》时[1],有个例子的原理被广泛讨论——
(最佳奖品问题) 假设我们可以从一系列先后宣布的n个不同的奖项中选取一个,在一个奖项宣布后我们必须立刻决定是接受还是拒绝转而考虑随后的奖项。我们只能根据该奖项与前面已经宣布的奖项的比较决定是否接受它。就是说,例如,当第5个奖项宣布时,我们知道它与前面已经宣布的4个奖是如何比较的。假设拒绝了一个奖就失去了这次机会,我们的目标是使得到最佳奖的概率达到极大。假定奖项的所有n!个次序都是等可能的,我们该怎样做?
解 选定一个k,0≦k≦n,同时考虑前k个都拒绝并接受此后第一个比前面k个更好的策略,将使用此策略选到最佳奖的概率记为Pk(best)。为了计算它,对最佳奖项的位置X取条件,得出
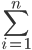 Pk(best|X=i)P(X=i)=
Pk(best|X=i)P(X=i)=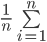 Pk(best|X=i)
Pk(best|X=i)现在,如果最佳奖项在前k个奖项之中,那么用所考虑的策略就选不到最佳奖。另一方面,如果最佳奖在位置i(i>k),那么当前k个的最佳奖也是前i-1个的最佳奖时,我们就可以选到最佳奖(因为在位置k+1,k+2,…,i-1中的奖项将都没被选取)。因此,我们看到
从上式我们得到

现在,如果我们考虑函数
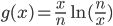
那么
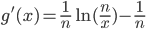
所以
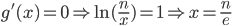
这样,因为Pk(best)≈g(k),我们看到所考虑的这类策略中的最佳策略,就是放弃前面的n/e个奖项,然后接受第一个比这些都好的一个奖。另外,因为g(n/e)=1/e,这个策略选取到最佳奖的概率近似地为1/e≈0.36788 。
一系列的问题都与这个最佳奖品问题的原理类似,如:麦穗问题[2]、相亲问题[3]、恋爱法则[4]、炮灰模型与微软钻石题[5],等等。
这一系列问题都是典型的“最佳止步”问题[6,7],学术上一般称作秘书问题[8]:一个经理从一群N个姑娘中雇用一名秘书,每次他会见一个姑娘,见面之后就决定接受或拒绝该姑娘,如果他拒绝了一个姑娘,以后他就不能再召见她了,每一次会见,经理能知道现在正在与他谈话的姑娘与她之前的姑娘相比可排在什么名次,但不知道把她与尚未见面的姑娘相比情况会怎样,我们假设他按随机的次序会见姑娘,问他应如何决定雇用哪一位姑娘,特别地,我们要找这样一个规则,它使选中N个姑娘中最好的一位的概率最大,或者使选中的姑娘的绝对名次的均值最小(1是最好的姑娘的名次,2是次好的名次,…,N是最差的名次)。
最优停时理论是概率论体系中一个具有很强的实用性领域,近年来,不少金融学家和金融数学家将这一理论与现代的投资组合理论相结合,取得了不错的成绩。但是这一领域的研究文献仍然不多,该领域仍处于起步阶段。Pliska SR and Selby MJ 首次运用该理论研究了具有固定交易费用的证券投资决策问题,写出了具有两个证券投资决策问题的一种简单算法。Bernard Dumas and Elisa Luclano(1998)在此基础上,进一步运用最优停时理论(Optimal-stopping literature)考察了有交易费用时投资组合的动态最优策略,并且求解出精确的数值解。国内关于最优停时理论在金融数学和金融学中的应用研究文献暂时处于空白[9]。
[1] Ross, Introduction to Probability Models (中文版《应用随机过程:概率模型导论》).
[2] http://episte.math.ntu.edu.tw/articles/sm/sm_03_05_1/
[3] http://cos.name/2012/03/find-right-one/#more-4897
[4] http://songshuhui.net/archives/57722
[5] http://blog.sina.com.cn/s/blog_79ecf69801013q41.html
[6] http://en.wikipedia.org/wiki/Optimal_stopping
[7] http://specoder.is-programmer.com/posts/29944.html
[8] 周元燊,等. 最优停止理论. 上海科学技术出版社, 1983.
[9] http://www.ectime.com.cn/Emag.aspx?titleid=8185
Speak Your Mind