一个赌徒在每次赌博中以概率p赢一个单位，并以概率q=1-p输一个单位，假设各次赌博都是独立的，赌徒在开始时有a个单位，问他的财富在达到0（即破产）前先达到N的概率是多少[1]？
设Pa(a=0,1,…,N)记赌徒在开始时有a个单位而且他的财富最终达到N的概率。通过对初始的一次赌博的结果取条件，我们得到
Pa = pPa+1 + q Pa-1, a=1,2,…,N-1
由于p+q=1，上式等价地有
pPa + qPa = pPa+1 + q Pa-1
或者
Pa+1 - Pa =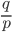 
(Pa - Pa-1), a=1,2,…,N-1
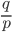(Pa - Pa-1), a=1,2,…,N-1由于P0 = 0，我们从上一式得到
P2 - P1 = 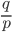(P1 - P0) = 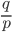P1
P3 - P2 =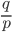(P2 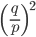- P1) = 
P1
Pa - Pa-1 =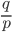(Pa-1 - Pa-2) = 
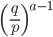P1
PN - PN-1 =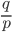(PN-1 - PN-2) = 
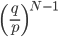P1
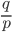(P1 - P0) = 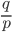P1P3 - P2 =
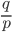(P2 - P1) = 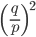P1Pa - Pa-1 =
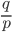(Pa-1 - Pa-2) = 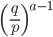P1PN - PN-1 =
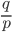(PN-1 - PN-2) = 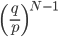P1将这些方程的前a-1个相加，得到
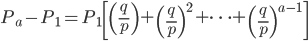
或
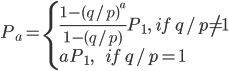
利用PN = 1，我们得到
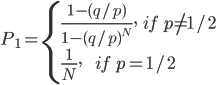
因此
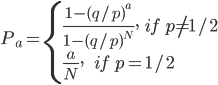
注意，当N->∞时：
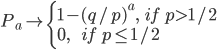
因此，若p>1/2，则存在一个正概率，赌徒的财富将无限地增长；而若p<=1/2时，则赌徒将（以概率1）在对阵一个无限富有的对手时破产。正所谓“久赌必输”，就算是一对一机会均等的赌局（p=1/2），要是一直赌下去的话，最终将会破产。 书籍[2]中对以上赌徒破产问题进行了比较深入的讨论，该书对赌徒破产概率的计算使用了差分方程的解法：
Pa = pPa+1 + q Pa-1
其中PN = 1，P0 = 0。对以上差分方程，令Pa = λa，得到
λa = pλa+1 + q λa-1
pλ2 - λ + q = 0
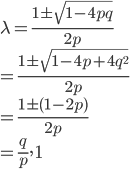
当p≠q时，差分方程有两个异根，因此Pa = C + D(q/p) a，C和D是常数。根据PN = 1，P0 = 0，得到
C + D(q/p) N = 1
C + D = 0
C + D = 0
解得
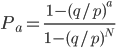
当p=q时，对上式取z = q/p趋近于1时的值：
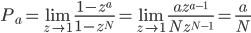
因此同样可得
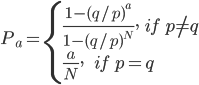
参考：
[1] Ross, Introduction to Probability Models (中文版《应用随机过程：概率模型导论》).
[2] Problem 5, Huygens and the Gambler’s Ruin. Classic Problems of Probability. Wiley, 2012.
[1] Ross, Introduction to Probability Models (中文版《应用随机过程：概率模型导论》).
[2] Problem 5, Huygens and the Gambler’s Ruin. Classic Problems of Probability. Wiley, 2012.
[...] 考虑赌徒破产问题，当赌徒初始有a单位财富，在每一次赌博中，他以1/2概率输掉1单位财富，以1/2概率赢得1单位财富，则他最后能赢得N单位财富的概率为a/N。以另一种角度考虑这个问题，假设进行了n次赌博后，赌徒有Kn单位财富，则再进行一次赌博后，他的财富期望值为 E(K_{n+1})=frac{1}{2}(K_{n}+1)+frac{1}{2}(K_{n}-1)=K_{n} ，即下一次赌博后的财富期望值等于目前的财富，这种性质在概率论中叫做鞅[2]。那么，当赌徒初始有a单位财富时，他进行了一次赌博后，他的财富期望值仍为a，如此进行了多次，直到赌徒破产（财富为0）或者财富增加到N单位，这一过程中赌徒的财富期望值一直是a，则令p为赌徒的财富能够达到N的概率，q为赌徒破产的概率，那么必定有： a=p times N + q times 0 ，从而推出 p=frac{a}{N} 。 [...]