蒙提霍尔问题，亦称为蒙特霍问题或三门问题（英文：Monty Hall Problem）[1]，是一个源自博弈论的数学游戏问题，大致出自美国的电视游戏节目Let's Make a Deal。问题的名字来自该节目的主持人蒙提·霍尔（Monty Hall）。
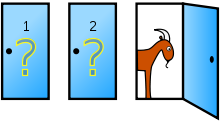这个游戏的玩法是：参赛者会看见三扇关闭了的门（X、Y、Z），其中一扇的后面有一辆汽车，选中后面有车的那扇门就可以赢得该汽车，而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门（例如X），但未去开启它的时候，知道门后情形的节目主持人会开启剩下两扇门的其中一扇（例如Y），露出其中一只山羊。主持人其后会问参赛者是坚持原来的选择（即X）呢，还是换另一扇仍然关上的门（即Z）。那么，哪一个选择赢得汽车的概率更大？
换另一扇门赢得汽车的概率更大，为2/3；而坚持原来的选择赢得汽车的概率为1/3。因此，更好的选择是“换”。
证明如下[2]：
令CX、CY、CZ分别代表门X、Y、Z藏有车的事件，令HY代表主持人打开门Y的事件。由于问题假定参赛者刚开始选择了门X，并且主持人后来打开了门Y，则只有当车在门Z时，换门才是一个更好的策略，即，参赛者换门而赢得车的概率为P{CZ|HY},根据贝叶斯定理，有：
在上面的计算过程中，我们假定，当主持人有两扇门可以打开时（即，车在门X后面），会等可能地打开任意一扇门；由于主持人不会打开有车的那扇门，所以有P{CY|HY}=0，因此
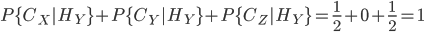
参考：
[1] http://zh.wikipedia.org/wiki/蒙提霍尔问题
[2] Problem 32："Monty Hall, Cars, and Goats". Classic Problems of Probability. Wiley, 2012.
[1] http://zh.wikipedia.org/wiki/蒙提霍尔问题
[2] Problem 32："Monty Hall, Cars, and Goats". Classic Problems of Probability. Wiley, 2012.
Speak Your Mind