浦丰投针问题可以根据条件概率进行计算,涉及到积分运算。在[1]的第1.1节中给出了另一种巧妙的解法,不仅使计算量大为减少,而且更加体现几何概率的思想。
令针长为L,平面上等间距相互平行垂直相交的平行线间距为D,且L<D。令X1为随机投掷到平面上长为L1的针与平行线相交的次数,当L1<D时,则X1只可取0或1(即要么不相交,要么相交)。
令pn表示针恰好与n根平行线相交的概率,且令E(X1)表示随机变量X1的期望值,则有:
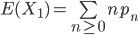
对于L1<D的情形,有:
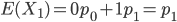
而p1正是我们所要求的针与平行线相交的概率。假如有另一根长为L2的针随机投掷,则该针与平行线相交的次数X2也是一个随机变量。随机变量X1和X2是相互独立的,除非它们焊接在一起。假如这两根针的一端焊在一起,则可以形成一根直线,或者形成一个角度,不管哪种情形,这两根针同时投掷到平面上,它们与平行线相交的次数仍然是X1+X2,此时随机变量X1和X2不再相互独立,但它们之和的期望值仍然满足可加性:
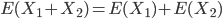
以此类推,当有k根针一端都焊在一起时,X1+X2+…+Xk仍满足式(\ref{F1})。
由于E(X1)依赖于L1,我们可以表示E(X1)=f(L1),其中f是某一个待定函数。通过把两根针的一端焊在一起形成一条直线,则有E(X1+X2)=f(L1+L2),并根据式(\ref{F1})可得:
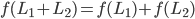
从而可推出f是线性函数。由于f随L的增大而单调增大,可推出对于L∈R+,有f(L)=rL,其中常数r待定。
考虑一条长为L的刚性线C随机地投掷到平面上,令Y为C与平行线相交的次数,而C可近似表示为多段线段拼接而成,因此Y约等于X1+X2+…+Xk,令k→∞,可得
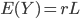
我们可以通过选取合适形状的线C来求得r的值。令C为直径D的线圈,则C恰好有2段小线段与平行线相交,于是E(Y)=2,L=πD,根据式(\ref{F2})可得:
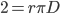
因此r=2/(πD)。从而对于长度L小平行线间距D的针,其与平行线相交次数的期望值(或相交的概率)为:
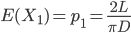
参考:
[1] Klain & Rota. Introduction to Geometric Probability (Lezioni Lincee). Cambridge University Press, 1997.
[1] Klain & Rota. Introduction to Geometric Probability (Lezioni Lincee). Cambridge University Press, 1997.
Speak Your Mind