泊松范式（Poisson paradigm）

参数为λ的泊松分布为

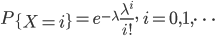
参数为n和p的二项分布为

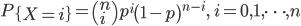
对于二项分布，当n很大、p很小时，令λ=np，则有

其中

于是，参数为n和p的二项分布当n很大、p很小时，可近似等于参数为λ=np的泊松分布：

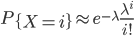
随机变量X的矩母函数φ(t)定义为

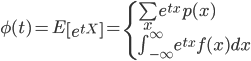
令随机变量X_i等于1若试验成功，否则为0，则成功的总次数X可表示为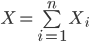，而X_i为伯努利随机变量，其矩母函数为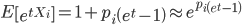

上式利用了此结论：当|x|很小时，有近似式e^x≈1+x。
由于独立随机变量之和的矩母函数等于各个随机变量的矩母函数之积，则有

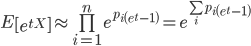
泊松分布的随机变量的矩母函数为

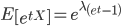
对比公式（\ref{F1}）和（\ref{F2}）可得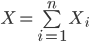，的分布可近似为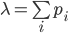的泊松分布。对于参数为n和p的二项分布，。
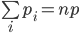当X的每次试验X_i之间并不相互独立、但相关性较弱时，X仍可近似为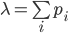的泊松分布。在《匹配问题》一文中，令A_i表示第i个标签匹配，有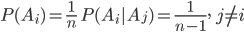

因此，尽管A_i和A_j之间并不独立，但它们之间的相关性随着n的增大而减弱：P(A_i|A_j)≈P(A_i)=1/n。从而当n很大时，匹配个数近似服从于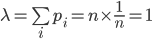的泊松分布。

以上的结果被称为泊松范式（Poisson paradigm）：

在n次试验中（n很大），若每次试验的成功概率p_i很小，且相互独立或者几乎相互独立，则成功的次数X近似服从于的泊松分布，特别地，P{X=0}=e^-λ。