样本空间与概率定义

集合运算

交换律

结合律

分配律

德•摩根定律

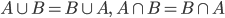
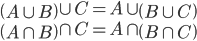
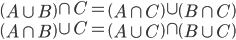
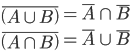
概率的公理化定义

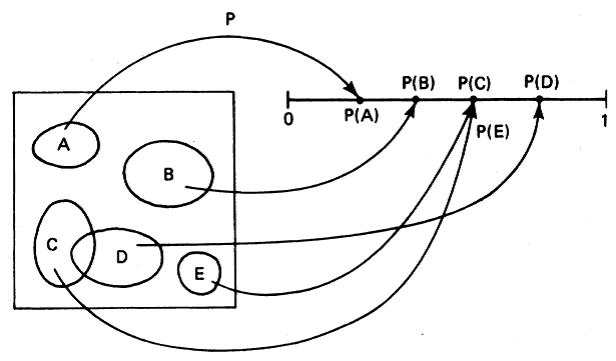
在样本空间Ω上的概率测度是该样本空间子集的一个映射函数，并且满足以下三条公理（概率论公理化定义）：
（一）对于任意一个子集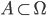，它的映射函数的值是一个非负数：；
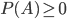（二）对于任意两个不相交的子集A和B，它们的并集的映射函数的值等于各自的映射函数的值之和：P(A + B) = P(A) + P(B)；
（三）样本空间Ω的映射函数的值为1：。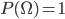

从以上三条公理可以推导以下结论：
（1）对于任意集合A，有；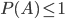
（2）若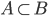，则B等于不相交的A和的并集，根据公理一和二有：

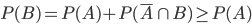
（3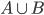）和B可分别表示为不相交的两个子集的并集：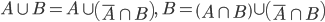

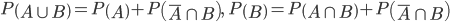
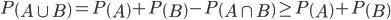
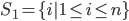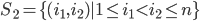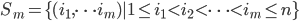根据公理二可得：

由以上两式可得：

进一步得：

令，，，则根据数学归纳法可得：

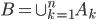上式的另一种推导如下： 令X_i为一随机变量，当A_i发生时，X_i=1，否则X_i=0。令，则 等价于所有随机变量X₁,…,X_n全为0，即随机变量Y=(1-X₁)(1-X₂)…(1-X_n)等于1，而Y的取值只能是0和1，所以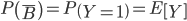，所以：

其中：