Sherman-Morrison-Woodbury公式的证明

首先证明Sherman-Morrison公式：

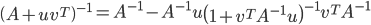
其中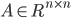，非奇异，即A^-1存在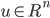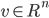，，。SM公式看似复杂，但可以通过求解以下线性方程组来推导出来：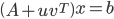

式（\ref{2}）两边同时乘以A^-1，令 A^-1u=z 和 A^-1b=y，则有：

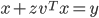
注意到v^Tx是标量，令α=v^Tx。式（\ref{3}）两边同时乘以v^T，得：

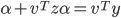
由于式（\ref{4}）中v^Tz和v^Ty都是标量，从而由式（\ref{4}）可解得：

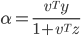
由式（\ref{3}）和y、z、α的定义可得：

由（\ref{2}）和（\ref{6}）即可得Sherman-Morrison公式，即（\ref{SM}）。

由Sherman-Morrison公式，并令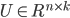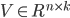， ，可得：

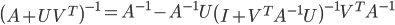
上式即为Sherman-Morrison-Woodbury公式。可以看到，Sherman-Morrison公式是Sherman-Morrison-Woodbury公式在k=1时的特殊情形。

如何证明Sherman-Morrison-Woodbury公式？式（\ref{7}）两边同时乘以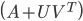，并证明两边均等于单位矩阵I即可。