参数为λ的泊松分布为
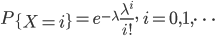
参数为n和p的二项分布为
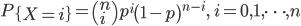
对于二项分布，当n很大、p很小时，令λ=np，则有$$!\begin{array}{l} P\lef[......]
样本空间与概率定义
集合运算
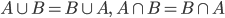
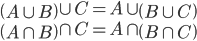
$$!\begin{array}{c} \left( A\cup B \right)\cap C=\left( A\cap C \right)\cup \left([......]
赌徒破产问题
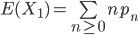
一个赌徒在每次赌博中以概率p赢一个单位，并以概率q=1-p输一个单位，假设各次赌博都是独立的，赌徒在开始时有a个单位，问他的财富在达到0（即破产）前先达到N的概率是多少[1]？
设Pa(a=0,1,…,N)记赌徒在开始时有a个单位而且他的财富最终达到N的概率。通过对初始的一次赌博的结果取条件，我们得到
Pa = pPa+1 + q Pa-1, a=1,2,…,N-1
由于p+q=1，上式等价地有
pPa + qPa = pPa+1 + q Pa-1
或者
Pa+1 - Pa = 
(Pa - Pa-1), a=1,2,…,N-1
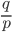(Pa - Pa-1), a=1,2,…,N-1由于P0[......]
匹配问题
以下的第一个匹配问题摘自[1]：
问题：假如你有一个装了n个无差别的球的罐子，每个球分别贴了1,2,3,…,n的标签。每次取出一个球直至所有球均取出，那么，至少有1个球的取出顺序与它的标签一致的概率是多少（例如，标签为2的球是第2个取出来的）？
解答 n个球有n!种排列顺序，假设在某一排列中第j个元素代表第j个取出的球。令Pj(j=1,2,…,n)代表某一给定的排列的第j个取出的球的标签为j，并且令Aj代表具有属性Pj的排列的集合。那么，至少有1个球的取出顺序与它的标签一致的排列的数量Ln为
$$! \begin{array}{l} {{L}_{n}}=|{{A}_{1}}\cup {{[......]
Dice Roll
连续抛掷一枚标准的骰子（即出现6种点数的概率一样，均为1/6）直至点数和超过12。则点数和最有可能是多少？例如，如果点数依次为3、6、1、5，则点数和为15。
解 一种解法是穷举所有点数系列，看看哪个点数和最有可能。但有另一种更巧妙的方法。假如点数系列之和为14，则最后一次抛骰子的点数不可能是1，否则点数和为13（已经超过12）而终止。对于产生14的所有点数系列，如果最后一次的点数均减少1，则可以产生13（因得到14的最后一次不能是1，所以得到14的最后一次骰子点数只能是2、3、4、5、6，那么若最后一次骰子点数改为1，2，3，4，5，这些点数系列之和就会得到13），因此，出现点数和为[......]
转载：《狼来了》的概率论解读
伊索寓言《狼来了》可谓家喻户晓。那个说谎的孩子是怎样一步一步丧失村民的信任的呢？借助于贝叶斯公式我们可以给出故事的概率论解读。
记A为事件“这个小孩说谎”，B为事件“这个小孩被认为可信”；再不妨设可信的孩子说谎的可能性为0.1，不可信的孩子说谎的可能性为0.5，即
原来，村民们对这个小孩的印象是
$$! \begin{equation} \label{F2} P(B)=0.8,\quad P(\overline[......]
浦丰投针问题（Buffon’s Needle Problem）
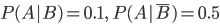
浦丰投针问题（Buffon’s Needle Problem）是几何概率的经典问题之一，由George-Louis Leclerc和Comte de Buffon于1777年提出——平面上画有等距离为D（D>0）的无限多条平行线，向此平面投掷一根长度为L（L≤D）的针，则该针与任一平行线相交的概率Pcut为：
重复进行投掷的试验，记下试验总次数Nd和针与平行线相交的次数Nc，则利用以上公式可以近似求得圆周率π：
$$!\pi =\frac{2L}{{{P}_{cut}}D}\approx \frac{2L}{({{N}[......]
斯特林公式的概率证明
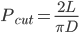
斯特林公式[1]是用来求n阶乘的近似值，公式如下：
该公式的一种概率证明方法如下[2]。令X1，X2，...，Xn是独立的泊松分布随机变量，均值都是1，令
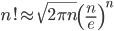
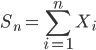，则Sn的均值和方差都是n。$$!\begin{array}{l} P\{{{S}_{n}}=n\}=P\{n-1[......]
单位区间[0 1]里随机分布n个点
在数轴上的区间[0 1]上有两个随机点A和B，它们的坐标服从[0 1]上的均匀分布，即X1~U(0,1)，X2~U(0,1)。则此两点间距离的数学期望是多少？
两点间的距离X = |X1-X2| = max{X1,X2} - min{X1,X2}。令Y = max{X1,X2}， Z = min{X1,X2}，两者的累积分布函数为：
F(Y) = P(Y≦y) = P(X1≦y & X2≦y) = P(X1≦y) × P(X2≦y) = y×y = y2
F(Z) = P(Z≦z) = 1-P(Z≧z) = 1-P(X1≧z & X2≧z) = 1 - P(X1≧z) × P(X[......]