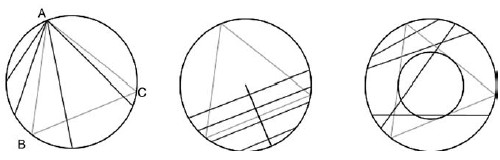
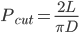浦丰投针问题可以根据条件概率进行计算，涉及到积分运算。在[1]的第1.1节中给出了另一种巧妙的解法，不仅使计算量大为减少，而且更加体现几何概率的思想。

令针长为L，平面上等间距相互平行垂直相交的平行线间距为D，且L<D。令X₁为随机投掷到平面上长为L₁的针与平行线相交的次数，当L₁<D时，则X₁只可取0或1（即要么不相交，要么相交）。

令p_n表示针恰好与n根平行线相交的概率，且令E(X₁)表示随机变量X₁的期望值，则有：

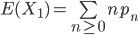
对于L₁<D的情形，有：
$$!E(X_1)=0{p_0}+[......]

阅读全文 »

浦丰投针问题（Buffon’s Needle Problem）是几何概率的经典问题之一，由George-Louis Leclerc和Comte de Buffon于1777年提出——平面上画有等距离为D（D>0）的无限多条平行线，向此平面投掷一根长度为L（L≤D）的针，则该针与任一平行线相交的概率P_cut为：

重复进行投掷的试验，记下试验总次数N_d和针与平行线相交的次数N_c，则利用以上公式可以近似求得圆周率π：
$$!\pi =\frac{2L}{{{P}_{cut}}D}\approx \frac{2L}{({{N}[......]

阅读全文 »