首先证明Sherman-Morrison公式:
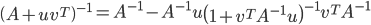
其中,
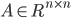 非奇异,即A-1存在,
非奇异,即A-1存在,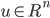 ,
,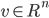 。SM公式看似复杂,但可以通过求解[......]
。SM公式看似复杂,但可以通过求解[......]
Random Walk in VAR
浦丰投针问题可以根据条件概率进行计算,涉及到积分运算。在[1]的第1.1节中给出了另一种巧妙的解法,不仅使计算量大为减少,而且更加体现几何概率的思想。
令针长为L,平面上等间距相互平行垂直相交的平行线间距为D,且L<D。令X1为随机投掷到平面上长为L1的针与平行线相交的次数,当L1<D时,则X1只可取0或1(即要么不相交,要么相交)。
令pn表示针恰好与n根平行线相交的概率,且令E(X1)表示随机变量X1的期望值,则有:
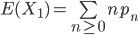
斐波那契数列[1]指的是这样一个数列:0、1、1、2、3、5、8、13、21……,每一项是其前面两项之和,即有通式:F0=0,F1=1,F2=1,Fn+2=Fn+1+Fn(n∈非负整数)。
下面通过线性代数的方法来求得斐波那契数列的通式Fn。
令 ,则
,则 !......]
!......]
浦丰投针问题(Buffon’s Needle Problem)是几何概率的经典问题之一,由George-Louis Leclerc和Comte de Buffon于1777年提出——平面上画有等距离为D(D>0)的无限多条平行线,向此平面投掷一根长度为L(L≤D)的针,则该针与任一平行线相交的概率Pcut为:
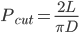
斯特林公式[1]是用来求n阶乘的近似值,公式如下:
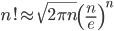
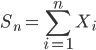 ,则Sn的均值和方差都是n。
,则Sn的均值和方差都是n。Copyright © 2024 · 电亮人生 · Copyblogger Theme · WordPress · Log in